Les notions sur les vibrations nécessaires et suffisantes pour comprendre les calculs simples présentés pour isoler un équipement.

Le bruit est une mise en vibration des particules. Cette vibration peut alors se propager dans l’air, dans une structure (comme une paroi), dans un liquide (vagues sur l’eau)…
L’appellation « vibration » est généralement dédiée à un phénomène visible et qui peut être ressenti par contact. Mais le bruit est une vibration invisible.
Ainsi, une paroi excitée par le bruit se comporte comme un haut parleur et génère à nouveau des ondes dans l’air, donc du bruit.
Exemple : une discothèque en sous-sol excite les parois qui font haut-parleur dans les locaux au dessus, jusqu’aux étages élevés.
Donc, un bruit est une vibration et une vibration génère systématiquement un bruit qui peut être trop faible pour être entendu. A noter qu’une vibration est généralement « entendue » avant d’être perceptible au touché.
LA FREQUENCE PROPRE
Tout élément a une fréquence « naturelle » de mouvement qui lui est propre.
Lorsque l’on excite le LA d’une corde de guitare, elle vibrera toujours à 440 Hz. C’est la fréquence propre de cette corde.
Prenons l’exemple d’une balançoire excitée par une bourrasque de vent ou car vous l’avez tirée et relâchée. Cette balançoire se mettra à osciller toujours à sa même fréquence propre. A cette fréquence, le mouvement n’est pratiquement pas atténué, sauf par les forces de frottement (air, fixations..) qui finiront par l’arrêter.
LA FREQUENCE DE RESONANCE
Mais si vous entretenez le mouvement à cette même fréquence (action au moment où la balançoire change de direction), les énergies vont s’additionner et le mouvement s’amplifier, au point qu’il puisse devenir dangereux ! Il y a alors résonance et fréquence d’excitation = fréquence propre (ces 2 termes sont souvent confondus).
Chaque élément ou système a plusieurs fréquences propres (verticale, horizontales, de torsion), que ce soit les organes (et oui !) ou les ponts !
Exemples de mises en résonance
Les exemples de ponts mis en mouvement par des rafales répétées de vent ne sont pas rares, avec la tristement célèbre chute du Pont de Tacoma.
Chute du Pont de Tacoma from LadHyX on Vimeo.
Si les structures sont bien calculées, elles peuvent tenir !
Un bâtiment a des fréquences propres de quelques Hz comme celles d’un tremblement de terre. Au cours d’un tremblement de terre, ces mêmes fréquences se conjuguent ! Il se produit alors un phénomène de résonance, amplifiant les mouvements du bâtiment. C’est toujours très impressionnant tel que le montre la vidéo ci-après (le chargement peut prendre un peu de temps !).
CALCUL DE PLOTS ANTIVIBRATOIRES
La croyance collective conduit à penser qu’il suffit de mettre en place un matériau souple de type caoutchouc pour résoudre un problème de vibrations sous un équipement.
Il est souvent fait référence au silentbloc (marque déposée par PAULSTRA) qui sont des plots antivibratoires parmi d’autres.
Pensez vous que les mêmes suspensions puissent être mises en oeuvre sous un camion et une voiture ?
On imagine bien que celles de la voiture risquent d’être écrasées et non efficaces pour le camion !
Le poids va donc être un élément parmi d’autres. Et un mauvais choix peut conduire à une efficacité nulle, au pire à une amplification.
Pour comprendre, il faut revenir à la fréquence propre d’un élément. Comme tout élément, un plot antivibratoire a une fréquence propre (qui doit être donnée par le fournisseur).
Analyse de la courbe de la fréquence propre
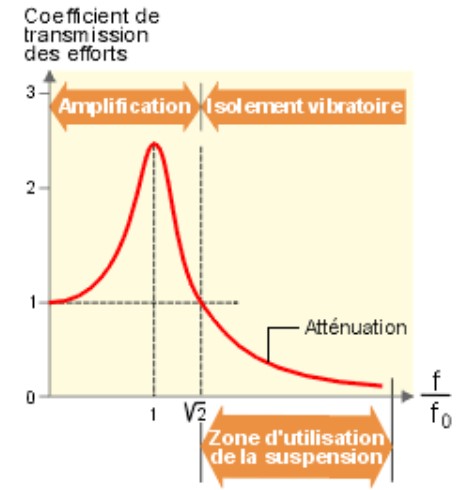
Le graphe ci-contre (issu du site energiepluslesite) présente la courbe du comportement de la fréquence propre.
A la fréquence fo (1 sur l’axe des abscisses), l’amplification est maximum. En fait, elle dépend de l’amortissement du matériau. Pour un matériau non amorti, elle est infinie ! En pratique, les systèmes parmi les moins amortis sont les ressorts.
Avant cette zone, on voit que le coefficient d’amplification est de 1. Autrement dit, le matériau se comporte comme une cale dure (ni amplification, ni atténuation).
L’atténuation ne commence qu’au delà de Racine2*fo = 1,414*fo.
Si l’on pose une machine avec une fréquence excitatrice f, il faudra donc que les plots sélectionnés soient caractérisés par une fréquence propre bien en dessous de f (voir exemple de calcul ci-dessous).
Amortissement vibratoire
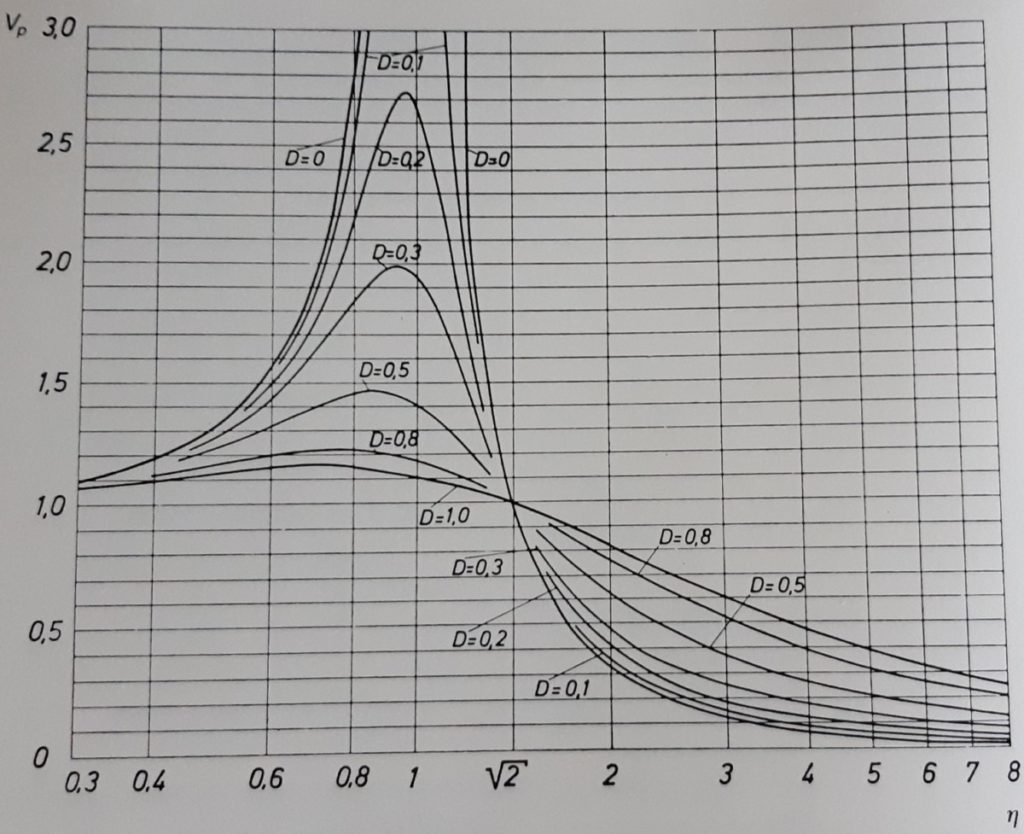
Les courbes ci-contre (doc GERB) montrent l’influence de l’amortissement (D = taux d’amortissement critique).
Un taux faible est représentatif du comportement d’un ressort pur, ce qui permet une forte atténuation mais peut poser problème d’amplification à la fréquence de résonance.
L’ajout d’amortissement limite la résonance mais limite également l’atténuation des vibrations.

On voit bien ici le ressort qui atténue les vibrations et l’amortisseur (en rouge) qui va limiter le débattement du ressort. Souvent l’amortisseur est intégré dans le ressort.
Taux de filtrage vibratoire
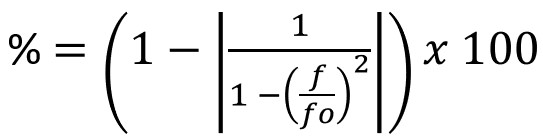
Le taux de filtrage se calcule en % à l’aide de l’équation ci-contre, pour un système sans amortissement.
Il sera donc inférieur avec de l’amortissement.
Exemple de calcul simplifié de plots antivibratoires
Considérons une machine tournant à 1500 tr/mn, ce qui est assez courant. La fréquence correspondant à cette vitesse sera f = 1500/60 = 25 tr/s = 25 Hz (voir notions d’acoustique).
Considérons que cette machine pèse 100 kg et que nous plaçons 4 plots recevant la même charge de 100/4 = 25 kg.
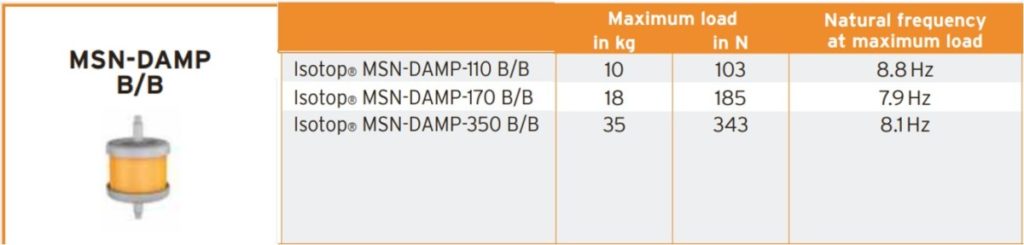
Nous pourrons retenir 4 plots antivibratoires de type « Isotop MSN-DAMP-350B/B » à base de matériau élastomère Sylomer de la marque Getzner, supportant au maximum 35 kg chacun.

Pour cette charge de 35 kg, leur fréquence propre est de 8,1 Hz.
Mais notre charge n’est que de 25 kg par plot. L’analyse des courbes détaillées montre que pour 25 kg (environ 250 N), leur fréquence propre sera de 9 Hz.
Avec notre fréquence d’excitation f de 25 Hz et la fréquence propre fo des plots de 9 Hz, le taux d’atténuation calculé est de 85 % avec l’équation ci-dessus, sans amortissement. Ces plots intègrent quelques % d’amortissement, du à leur nature élastomère. Cependant, ici cela a un impact faible sur le résultat.
85 % de filtrage, ce peut être suffisant pour une petite machine ne générant pas de forces importantes ou dans un environnement peu sensible. Dans les autres cas, il pourra être recherché d’avantage de filtrage, conduisant alors à utiliser des boites à ressorts pour obtenir fo plus faible.
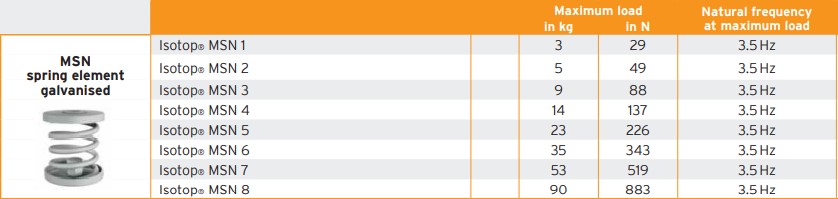
Le type de boite à ressorts ci-contre est caractérisée par une fréquence propre de 3,5 Hz. Le taux d’atténuation passe alors à 98 % !
Synthèse
Un plot antivibratoire se calcule en fonction de la fréquence que l’on doit filtrer et du poids de la machine.
Les plots doivent être suffisamment chargés (selon la plage annoncée par le fournisseur), ce qui explique que les plaques ne sont généralement pas efficaces, car la charge au cm2 devient trop faible.
Pour obtenir une efficacité d’au moins 95 %, il faut que la fréquence propre des plots soit au moins 5 fois inférieure à la fréquence excitatrice de la machine à filtrer.
Cela peut imposer des boites à ressorts dont les fréquences propres descendent à quelques Hz.
Les matériaux amortis, à base d’élastomère, sont limités généralement à plus de 10 Hz.

Dans le cas d’un régime moteur partant de 0 pour arriver à quelques centaines de Hz (comme un moteur de voiture, de pompe, de ventilateur…), l’amortissement est nécessaire pour éviter une forte amplification au moment du passage sur la fréquence propre des plots supportant le moteur. D’ailleurs, lorsque ces plots sont usés et à changer, on perçoit ce passage qui secoue la voiture au démarrage.
Il faut bien évidement que les gaines et canalisations soient également désolidarisées, au risque de transmettre les vibrations, au pire de casser.